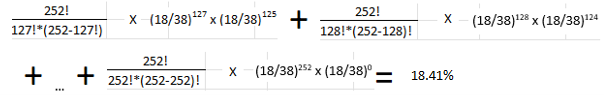Many prospective clients that we work with do not have any investments saved since they believe that the stock market is akin to gambling. I would like to take some time to illustrate why that sentiment is wrong and how probability, Roulette, and financial planning are all (somehow) related to each other.
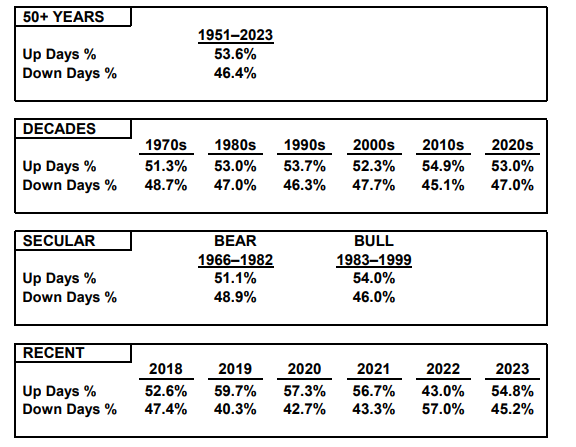
The chart below highlights the fact that the stock market had a 53.6% chance of having an up day (as measured by the S&P 5001) on any given day between 1951-2023.
Source: https://www.crestmontresearch.com/docs/Stock-Yo-Yo.pdf
Now let’s compare that to my favorite game in Las Vegas, Roulette. I wouldn’t call myself a gambling person, but it’s my favorite game since I know the odds and I know when to walk away. Every time I go to Vegas, I do the same thing. I go to the nearest Roulette table, bet $20 on black, play one round, and quit for that trip. If I win, great. I’m up $20 and may go and buy a tacky souvenir shirt I probably wouldn’t have if I didn’t win that game of Roulette. If I lost, then that meant one of the meals that would be the buffet at The Cosmopolitan might now just be McDonald’s. Annoying, but I’ll survive.
This is because, in Roulette, my odds of winning and doubling my money are 18/38 (or 47.4%) since there are 38 possible numbers (1-36 alternate between red and black, 0, and 00 which are uncolored) that the roulette wheel could hit. That is slightly worse than either a coin flip (50%) or earning a positive return in the stock market in a given day (53.6%). However, people rarely play one game of Roulette and people rarely invest only one day in the market. Over time, the stock market over the long-run looks less like thoughtless gambling and more like a thoughtful strategy. If we look at the odds of having a positive return in the stock market over one-year, three-year, five-year, or ten-year periods, the odds of betting on the stock market over the long term look more favorable.
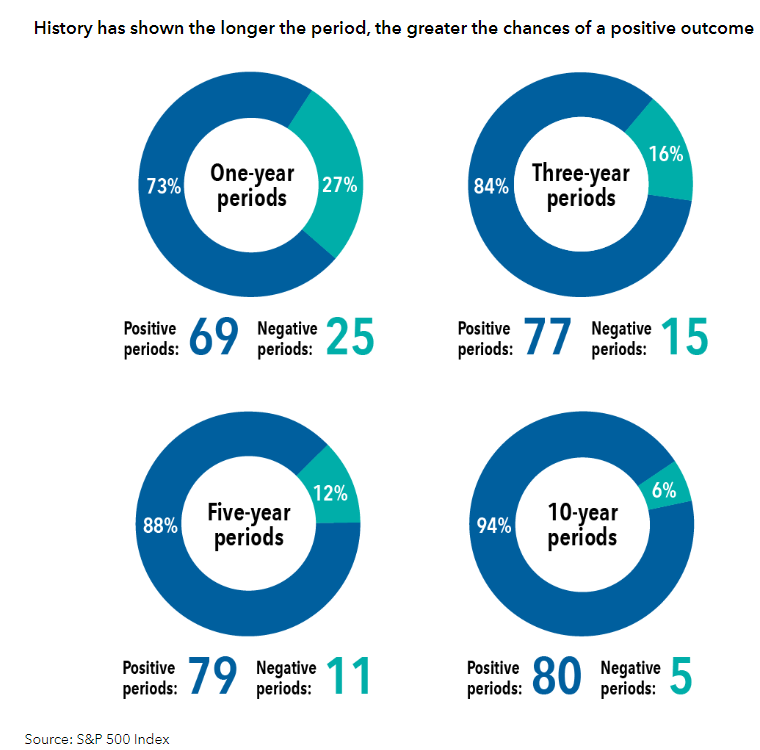
As an example, look at the one-year return illustrated in the infographic. The stock market was positive 73% of the time. There are 252 trading days in a year. Now, what are the odds that you will have more money than you started with in Roulette if you play the game 252 times my boring way of betting on black every time as measured by winning more times than you lose? We are looking to see if we win at least 127 times of 252 games. The answer is 18.41%. Quite a far cry from the 73% that the stock market can do over 252 trading days in a year. For the math nerds like me out there who are interested, you’ll find my work on how I got that answer of 18.41% in the appendix of this blog post.
Funny enough if you play 2 games of Roulette and want to know the odds of winning at least once, the answer is 49.86%. The casinos know that and that’s how they get you. I just said that the odds of winning in any one game with my bet on black is 18/38 or (47.4%). Say you win at least once in your two games of Roulette. You’re feeling good, you order yourself a drink, and you sit down for a third game. The chances of you winning 2 out of three games is 35.43%. After that, the odds just continue to cascade downwards out of your favor. Lower than if you just played one game.
This is why time spent in the market is much more important than trying to time the market. The former you can control, but the latter you can’t. Over long periods, investing in the stock market looks less and less like gambling until they no longer resemble each other. If you are looking to retire soon, your retirement could last 20 years, 30 years, or longer, and not investing to help fund that long of a retirement is more of a gamble than going to Vegas and betting it all on black.
I’m sure you are asking yourself, “What does any of this have to do with financial planning?”. Well, I’m glad you asked. In financial planning, we get a multitude of different questions from clients but the question that we get like clockwork is simply, “Do I have enough money to not outlive my retirement?”. To answer that question, we need to do a deep dive into that person’s finances (current spending, current assets and liabilities, goals for retirement, etc.) and run a Monte Carlo simulation on their financial plan.
What is Monte Carlo Simulation?
A Monte Carlo simulation when used with financial planning is essentially running the financial plan until its end, repeating it many times (usually a thousand or ten thousand scenarios), randomizing the returns on the investments based on historical performance of the asset class for each scenario, and counting how many scenarios came back with a positive number at the end of the financial plan and dividing it by the total number of scenarios ran in the financial plan. The percentage of total positive outcomes divided by the total number of scenarios ran in the simulation is your probability of success (as measured here by having enough money to not outlive your retirement) for your financial plan. Essentially, doing a Monte Carlo simulation on a financial plan is just like playing a very long series of games of Roulette. Successful financial plans typically “bet” on most of the numbers on the roulette table and unsuccessful financial plans generally bet it all on black, or worse, just bet it all on one number.2 To illustrate how this works in a financial plan, I have the following example.
Example
Rusty and Emily Griswold are both age 64, live in California, and want to retire next year. They meet with a financial planner to make sure they can get the answer to their only question, “Do we have enough money to not outlive our retirement?”. They have the following assets and profile:
- Emily’s IRA of $1,000,000.
- Rusty’s IRA of $1,000,000.
- A joint taxable investment account of $500,000.
- Rusty earns $48,000 per year.
- Emily earns $48,000 per year.
- Both Emily’s and Rusty’s Social Security start at their full retirement age (age 66 and 10 months) and will be projected to be $20,052 each per year. The income from social security is projected to increase by 2% each year.
- They would like to see the plan run until they are age 95.
- Their investment accounts are projected to earn a 5.55% return and are in a mix of 60% stocks and 40% bonds.
- They want to spend $12,000 per month. They also want to assume that their spending will increase by 3% each year.
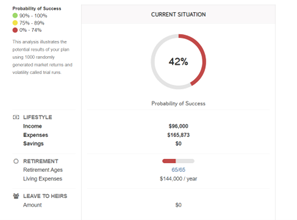
Their financial planner completes their financial plan and runs a Monte Carlo simulation for 1,000 different scenarios and estimates the probability of their financial plan’s success below:
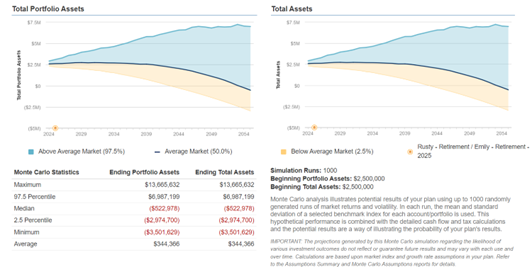
Rusty, Emily, and their financial planner then have the following conversation:
The Financial Planner: As illustrated by these graphs, you have a 42% chance of not outliving your retirement. The investments at the end of the plan can be anywhere from as high as $13,665,632 or as low as -$3,501,629. The average ending portfolio value is negative, as illustrated by the black line in the above graph. Put another way, the average scenario we ran came back with an unsuccessful financial plan. This is a large number of outcomes that can occur with your financial plan that are unfavorable to you. I recommend two changes. Look into retiring at 66 and reducing your spending to $11,000 per month.
Rusty: “But I don’t want to make any changes. 42% chance of success? Well, I guess that means that we should go to Vegas, play some Roulette, and bet it all on black! After all, the chances of winning with that Roulette strategy are higher at 47.4% as you pointed out earlier. I’d rather not reduce our spending and I want to retire at 65. C’mon Emily, I’m feeling lucky! Let’s go take a Vegas Vacation!3
Emily: “Hold on, Rusty! This is our retirement we’re talking about here. You can’t just go to Vegas, gamble all of our retirement savings, win a bunch of money and cars like you did 30 years ago (that’s how they originally got the funds for their joint taxable account), and call that our retirement plan. Remember what happened to your dad, Clark, 30 years ago? He had to ask his cousin Eddie for money just so he could get back home safely after losing $22,600. He lost almost everything in Vegas.”
Emily (To the Financial Planner): “In all seriousness, what options do we have to increase our odds of success?”
The Financial Planner: “As I was saying, you could instead retire at age 66 and reduce your spending to $11,000 per month. Here is a Monte Carlo simulation for that scenario:”
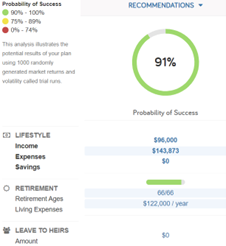
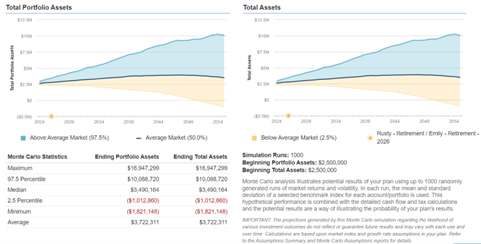
The Financial Planner: “The financial plan has to prognosticate a 30-year retirement, but keep in mind that many different things could happen in your lives between now and then. We can make changes to your investments over time and adjust your spending with how the market performs. The average scenario run leads to a positive portfolio value. Assuming that you adhere to these recommendations, I have little concern with the outcome of your retirement plan in my opinion.”
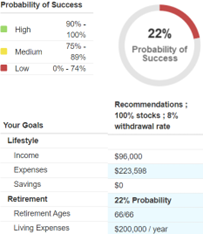
Emily: “I want to see a 100% probability of success. I don’t feel that 91% is good enough for me.”
The Financial Planner: “It’s now important to stress what Monte Carlo simulation is good for and also why you shouldn’t be reliant on it for everything in financial planning. Since we are only doing it 1,000 times, it cannot account for any improbable black swan events that even though they are extremely unlikely to happen, could happen. You can’t run an infinite number of scenarios in a Monte Carlo simulation. This is why there is no true 100% probability of success when it comes to any financial plan. If you want to see a scenario of 100% probability of success in the financial plan, I could assume that you are invested in a portfolio of 100% stocks that earns 12% per year.”
Emily: “Sounds good, but I don’t think that a 12% annual return in the stock market is realistic. Plus, it’s probably not appropriate to have me and Rusty in 100% stocks our entire retirement. Especially when we get to our 80s and 90s.”
The Financial Planner: “I agree. However, you wanted to see that scenario, so here it is.”
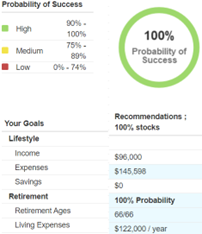
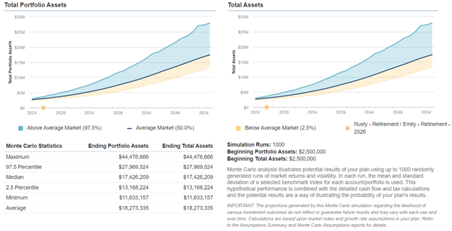
The Financial Planner: “Even though it shows a 100% probability of success, any unforeseen event could derail your financial plan. The higher the assumed return, the greater the variability of the potential value of your investments at the end of the financial plan. This is why the assumptions we use in a financial plan are just as important as how many times we run the Monte Carlo simulation.”
Rusty: “Eh, a 12% annual return assumption is good for me. That guy on YouTube said that we can expect the stock market to return 12% every year. He also said we can withdraw 8% from our portfolio each year and we’ll be fine.4 Is that true? If so, why are you only having us withdraw 5.28% from our portfolio each year?”
The Financial Planner: “I’ll run a scenario to show you why his comments on his YouTube show on the stock market can be a destructive way to think about retirement planning. I’ll do it by showing you that if you withdraw 8% per year (or $16,667 per month), you’ll have a worse probability of success than if you just retired next year and continued to spend $12,000 per month. Even with a 12% annual return.”
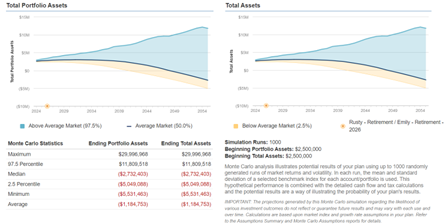
The Financial Planner: “As you can see here, the average scenario we ran came back with a negative portfolio value at the end of the plan (-$1,184,753). There is a huge range of outcomes with the highest end at $29,996,968 to the lowest end at -$5,531,463. It looks like under this scenario you would run out of money as soon as 15 years from now. With advances in medicine occurring every day and with people living longer on average, it is irresponsible planning to think retirement will only last 15 years. Even with retiring at 66 and reducing your expenses $1,000 per month like I recommended, withdrawing 8% per year means that you drop your rate of success from 100% to 22%.”
Rusty: “Thank you. I feel better that I understand why my current retirement plan doesn’t work and that with a few minor changes, like retiring one year later and reducing our spending by $1,000 per month, we can make our retirement plan work. Thank you.”
Emily: “Yes, thank you.”
The Financial Planner: “You’re welcome.”
Conclusion
I thought it would be fun to discuss how the Monte Carlo simulation got its name. Monte Carlo simulation takes its name from a 1913 incident at the Monaco casino, The Monte Carlo, where the gamblers at the roulette table watched in disbelief as the roulette wheel hit a black number 26 times in a row. They believed that the roulette wheel itself was rigged and that at some point there had to be a long streak of hitting red numbers in a row to balance out the long streak of black numbers that were hit in a row. However, the wheel itself was fine. Those gamblers instead just witnessed a truly amazing feat of probability at work. The odds of hitting black in roulette 26 straight times in a game of roulette is 1 in 67,108,864 (1 / (18/36)26). To compare, it’s somewhere in between the odds of being struck by lightning (1 in 15,300) and winning the Powerball jackpot (1 in 292,200,000). Extremely unlikely, but not impossible. This event was called the “Monte Carlo Fallacy” and was the inspiration for creating the statistical method of Monte Carlo simulation.
To subtly close, I would like to remind you not to leave your financial plan to a game of chance. I doubt that gambling on the game of “Successful Retirement” is one that you want to bet on. You can rig the retirement game in your favor by having a comprehensive financial plan done with our team of Certified Financial Planner™ (CFP®) Professionals, or if you already have a financial plan, have it reviewed by our team. Email us at financialplanning@bfsg.com or call us at 888-726-9378 to get the conversation started. Best of luck to you in your gambling adventures or your financial planning journey and always remember that “Past Performance is no Guarantee of Future Results”.
Footnotes:
- The S&P 500 Index is designed to be a leading indicator of U.S. equities and is commonly used as a proxy for the U.S. stock market.
- Another reason why diversification is a hallmark of any comprehensive investment plan.
- Rusty Griswold is the name of a character from the movie Vegas Vacation (1997): https://www.imdb.com/title/tt0120434/ starring Chevy Chase and Beverly D’Angelo.
- Dave Ramsey is a successful financial YouTuber and Radio Host whose shows are meant purely for entertainment and should not be misconstrued as financial advice. Here’s another article on why an 8% withdrawal rate doesn’t work: https://www.morningstar.com/retirement/an-8-retirement-withdrawal-rate
Disclosure: BFSG does not make any representations or warranties as to the accuracy, timeliness, suitability, completeness, or relevance of any information prepared by any unaffiliated third party, whether linked to BFSG’s website or blog or incorporated herein and takes no responsibility for any such content. All such information is provided solely for convenience purposes only and all users thereof should be guided accordingly. Please remember that different types of investments involve varying degrees of risk, and there can be no assurance that the future performance of any specific investment or investment strategy (including those undertaken or recommended by Company), will be profitable or equal any historical performance level(s). Please see important disclosure information here.
Additional Disclosures: The above Monte Carlo results and/or projections are based upon historical data and should not be construed or relied upon as an absolute probability that a different result (positive or negative) cannot or will not occur. To the contrary, different results could occur at any specific point in time or over any specific time period. The purpose of the projections is to provide a guideline to help determine which scenario best meets the client’s current and/or current anticipated financial situation and investment objectives, with the understanding that either is subject to change, in which event the client should immediately notify Benefit Financial Services Group (“BFSG”) so that the above analysis can be repeated.
Appendix:
To calculate the probability of winning the majority of games when playing Roulette 252 times by betting on black every single time, we need to compute the odds of winning at least 127 games, then winning at least 128 games, and so on, and add up all of those odds together. This can be show mathematically by the following formula:
P(x=127) + P(x=128) + … + P(x=252) = B
Where:
- P is the probability of our occurrence we want
- X is the number of games that we win with our bet
- B is our odds
- P(x=n) can be expressed in the following notation:
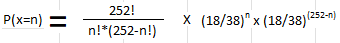
- Where (!) means the factorial of a number. A factorial of a number means a number gets multiplied by each succeeding whole number that is one less than itself until you get to 1. (For example, 3! Means 3 x 2 x 1 = 9, so 3! Is equal to 9. 4(!) means 4 x 3 x 2x 1 = 24, so 4! Is equal to 24, and so on). 0! Is defined to be 1.
Now we are equipped to solve the answer of “If we play 252 games of Roulette and bet on black every single time, what are our odds of winning at least 127 games of Roulette?”. We plug in the numbers to our formula and get the following answer: